 |
Case study: Theoretical bases
|
|
|
 |
This theoretical study reported here was prepared in relationship with the COMKISS European project.
Let us consider a ship which is undertaking voyages over a certain
relatively long period of time. The load she experiences and
consequently her response to this load are random and thus they would
be best analyzed by some reliable statistical methods. Clearly, from
the engineering point of view, the most important is to find an
accurate approach to study the extremal events occuring during this
period of exploration. The principal methodological challenge in the
so-posed problem comes from several different sources of the involved
random variation. They are directly related to temporal-spatial scale
within which one considers the sea surface. Yet, conditions
occuring on the sea surface are changing continuously in time and in
space, and the randomness is different in different scales and thus
different methods should be chosen depending on the scale and combined together.
Most of the material included in the considerations here appeared in some
form in the literature but this is, as far as we know, the first
attempt to put together the consistent methodological framework which,
as we hope, will be helpful for future advances in research on these
topics.
|
 |
 |
General description
|
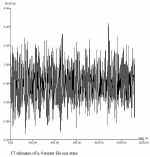
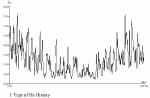
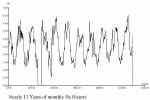
We consider the following three different scale
threshold levels. First, there is randomness related to short-time
variability of the sea surface in time intervals measured in minutes or
in few hours at most and in a restricted region in which the weather
conditions appear to be the same. Another level of variability is due
to the change of the sea states which is the consequence of changes of
weather conditions occuring within several hours or even several days
and also due to different conditions in distant regions of the sea.
Then there is a stochastic variability of different journeys which are
undertaken at different times and possibly along different routes. Of
course, these are only few of many possible factors and the complete
analysis would be extremely complex if possible at all. In these notes
we focus on these factors which are most important for the statistical
properties of extremal waves (or responses). However, the proposed
methods can be also applied to studies of arbitrary, not only extremal,
waves.
|
|
 |
Typical applications
|
In various practical problems, for example in safety considerations, it
is important to determine the probability that the response -- for instance
the heave amplitude, or the acceleration at a given location of a ship, or the
stress in a given member -- exceeds some critical level over some time interval
(one voyage, the duration of a storm, the lifetime of the vessel).
The concepts and notions which allow for the precise formulation of the
corresponding research problems are discussed in the report.
|
|
State of the Art - Old and new
|
|
 |
Present methodology
|
The conventional method is presently to oversimplify the problem, assuming that the random influencing variables are uncorrelated and of known simple distributions, and/or to use Monte Carlo type simulations of numerous potential histories for the time interval of interest, and accept the statistics of their results as a valid basis for the safety assessment.
|
|
|
 |
Recent improvements
|
Satellite measurements provide data at time intervals such that the conventional method of history reconstruction can not be used with them.
The report sets the definitions and theory for methods that rely on parameters which may be estimated from the satellite measurements.
|
|
|
 |
Analysis of the example
|
The following concepts and notions are defined and discussed:
 | Sea state and its duration. |
 | Route, as a time-indexed trajectory, and as an unknown variable apart from its end-points. |
 | Response process, on the basis of a conditional Gaussian model. |
 | Periods of stationarity. |
 | Distribution of response and probabilities of exceedances. |
 | Crossing intensity and oscillations density function. |
 | Height of the crest of an oscillation. |
 | Distribution of rainflow cycles. |
 | Poisson approximation for the number and the probability of exceedances. |
 | Connection of route segments. |
 | Estimation of the probabilities mentionned above. |
 |
Conclusions
|
 The
Theoretical statistical bases are set for analysis and estimation of response level exceedance and of rainflow damage accumulation experienced by a vessel. The
Theoretical statistical bases are set for analysis and estimation of response level exceedance and of rainflow damage accumulation experienced by a vessel.
|
|
|
|
 |
Research actions
|
 | The report raises many questions, and we refer the reader to it. |
 | The most important issues are the validation of the assumptions, and the practical estimation of the parameters used in the theoretical formulae.
Such practical estimation should not be limited to satellite data, but should of course consider them as one of the potential sources of information. |
|
|
 |
User persuasion
|
 | Safety assessment needs to be understood in a stochastic manner.
This is not yet current practice everywhere, but the models presented here are essentially stochastic, and they are a compelling stage in the process, all the more if satellite data are to be used. |
|
|
 |
Expected improvements
|
 | Collaborative research actions should be able to shed light on the ways to solve the problem of extracting information on the time-histories of sea state processes from the almost instantaneous space lines of the orbital path. |
|
|
Links and references
|
|
 |
The COMKISS project:
|
 Project objectives
Project objectives
The main objectives of the project are:
to demonstrate to major segments of the marine transport industry the
benefits of integrating satellite-derived information on sea state such as
wave height and direction.
to raise awareness of the usefulness of satellite data in increasing the
safety and overall efficiency of shipping operations by using the EWSE
(at CEO) as the principal channel for communicating progress.
The results should be of interest for enterprises such as ship certification, fast
ship/coastal traffic, and transportation of unconventional loads.
 Project partners
Project partners
Satellite Observing Systems , Godalming, UK
(David Cotton, project manager)
Mathematical
Statistics, Lund University, Sweden (Georg
Lindgren, project
co-ordinator)
Bureau
Veritas, Paris-La Defense, France (Guy
Parmentier)
Dockwise, Meer, Belgium (Cees Leenaars)
IFREMER, Brest, France
(Michel Olagnon)
OPTIMER, Brest, France (Raymond Nerzic),
Corsica Ferries, Bastia, France
 Project period
Project period
September 1, 1998 - August 31, 2000
|
Back to top | Back
to modules list
|




